| Term |
Page #* |
Information |
Images/Links |
| Symmetry elements |
73 |
Properties of symmetry of certain objects. Theses properties may include mirror planes, axes of rotation and inversion centers. |
Mirror plane and axis of rotation
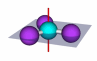 |
| Symmetry operations |
73 |
The actual reflection, rotation or inversion process across, around or through the symmetry element. |
|
| Group |
88-91 |
A set of values and operations that have the following properties:
- CLOSURE: If a and b are in the group then
a • b is also in the group.
- ASSOCIATIVITY: If a, b and c are in the group
then (a • b) • c = a • (b • c).
- IDENTITY: There is an element e of the group such
that for any element a of the group
a • e = e • a = a.
- INVERSES: For any element a of the group there is
an element a-1 such that
- a • a-1 = e
and
- a-1 • a - e
|
A good source on group theory is The Dog School of Mathematics at http://dogschool.tripod.com/
The definitions at left are from that site. |
| Group multiplication table |
|
A table listing all of the operations in a group applied to one another. The table demonstrates the closure of groups by showing that the result of any two operations is the same as another single operation within the group. |
|
| Point group |
79 |
The set of all symmetry operations for a molecule. |
|
| Mirror plane |
76 |
A mirror plane is a plane across which an object can be reflected so that the reflection corresponds to the the original object at that point. The the operation of reflection across a mirror plane is referred to as a  . A . A  v is a mirror plane that passes through the primary rotation axis and an outer atom. A v is a mirror plane that passes through the primary rotation axis and an outer atom. A  d is a mirror plane that does not pass through an outer atom. An exception to this is in Td and Dnd, in which all mirror planes are referred to as d is a mirror plane that does not pass through an outer atom. An exception to this is in Td and Dnd, in which all mirror planes are referred to as  d. A d. A  h is a mirror plane where the plane is perpendicular to the primary axis of rotation. Examples of h is a mirror plane where the plane is perpendicular to the primary axis of rotation. Examples of  v, v,  d and d and  h are at right. h are at right. |
 v v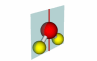
 d d
 h h |
| Rotation axis |
75 |
A rotation axis is an axis about which an object can be rotated. The operation of rotation is referred to as a Cn operation, where n is the number of divisions withing 360o that result in a match to the original form. The axis with the highest value of n is referred to as the primary rotation axis or highest order rotation axis. Examples of a C2 and C4 are at right. |
C2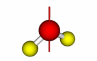
C4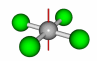 |
| Inversion center |
76-77 |
A point through which an object can be inverted and have the inverted form match the original. The operation is denoted i. SF6 is an example of this, the yellow S is the inversion center. |
SF6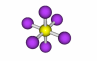 |
| Improper rotation axis |
77 |
An axis about which a molecule can be rotated, and then reflected across a  h mirror plane to yield a match to the original molecule. This operation is denoted Sn, where 360/n is the required number of degrees of rotation about the axis. This operation is also called a rotation-reflection operation. An example using TaF8 is at right; when turned 22.5o (360/8) and then reflected across the horizontal mirror plane, the resultant form matches the original h mirror plane to yield a match to the original molecule. This operation is denoted Sn, where 360/n is the required number of degrees of rotation about the axis. This operation is also called a rotation-reflection operation. An example using TaF8 is at right; when turned 22.5o (360/8) and then reflected across the horizontal mirror plane, the resultant form matches the original |
S8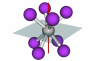 |
| Representation |
|
|
|
| Reducible representation* |
|
|
|
| Irreducible representation* |
|
|
|
| Class* |
|
|
|
| Character* |
91 |
The sum of the numbers on the diagonal of a square matrix, running from upper left to lower right. |
C2: 
Character
= (-1)+(-1)+1 = -1 |
| Character table* |
92 |
The complete set of irreducible representations for a point group. |
|
| Basis (for a representation, reducible or irreducible)* |
|
|
|
| Dissymetric |
96 |
The property of an object to not be superimposable on its mirror image. Also known as Chiral. An example using CHClFBr is at right. |


 |
| Asymmetric |
|
|
|
| Chirality |
|
|
|
| Hetero and homo-chiral |
|
|
|
| Criteria for evidence of a polar vector (dipole moment) |
|
|
|
| IR- and Raman active vibrational modes* |
|
|
|
| LCAO |
109 |
Linear Combination of Atomic Orbitals. This is done simply by adding the two atomic orbital wavefunctions together. |
 |
| Molecular overlap |
|
|
|
| Overlap criterion |
|
|
|
| Symmetry and energy constraints on overlap |
|
|
|
| Homonuclear diatomics |
|
|
|
| Heteronuclear diatomics |
|
|
|
| Bond Energy (De and Do) |
|
|
|
| Highest occupied molecular orbital (HOMO) |
126 |
The molecular orbital of highest energy that contains an electron. |
Please click here to go to a more in-depth explanation of HOMO and LUMO |
| Lowest unoccupied molecular orbital (LUMO) |
126 |
The molecular orbital of lowest energy that has a space available for an electron. |
| Bonding molecular orbital |
|
|
|
| Antibonding molecular orbital |
|
|
|
| Non-bonding molecular orbital |
|
|
|
| Frontier orbitals |
126 |
The HOMO and LUMO orbitals. These are known as such because they are at the outside of the molecule, and are the orbitals that determine the molecule's intereaction with other species. |
|











